Capacitors are connected together in series when they are daisy chained together in a single line
| Intro | Caps In Series | Series Caps Equation | Example 1 |
| Example 2 | summary |
Capacitors in Series

|
Capacitors in Series
Capacitors are connected together in series when they are daisy chained together in a single line |
 capacitors in series circuit
In the previous parallel circuit we saw that the total capacitance, CT of
the circuit was equal to the sum of all the individual capacitors added
together. In a series connected circuit however, the total or equivalent
capacitance CT is calculated differently.
In the series circuit above the right hand plate of the first capacitor, C1
is connected to the left hand plate of the second capacitor, C2 whose right
hand plate is connected to the left hand plate of the third capacitor, C3.
Then this series connection means that in a DC connected circuit, capacitor
C2 is effectively isolated from the circuit.
The result of this is that the effective plate area has decreased to the
smallest individual capacitance connected in the series chain. Therefore the
voltage drop across each capacitor will be different depending upon the
values of the individual capacitance’s.
Then by applying Kirchhoff’s Voltage Law, ( KVL ) to the above circuit, we
get:
capacitors in series circuit
In the previous parallel circuit we saw that the total capacitance, CT of
the circuit was equal to the sum of all the individual capacitors added
together. In a series connected circuit however, the total or equivalent
capacitance CT is calculated differently.
In the series circuit above the right hand plate of the first capacitor, C1
is connected to the left hand plate of the second capacitor, C2 whose right
hand plate is connected to the left hand plate of the third capacitor, C3.
Then this series connection means that in a DC connected circuit, capacitor
C2 is effectively isolated from the circuit.
The result of this is that the effective plate area has decreased to the
smallest individual capacitance connected in the series chain. Therefore the
voltage drop across each capacitor will be different depending upon the
values of the individual capacitance’s.
Then by applying Kirchhoff’s Voltage Law, ( KVL ) to the above circuit, we
get:
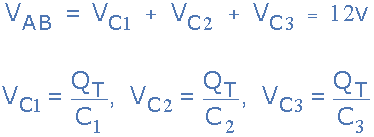 current through capacitors in series
Since Q = C*V and rearranging for V = Q/C, substituting Q/C for each
capacitor voltage VC in the above KVL equation will give us:
current through capacitors in series
Since Q = C*V and rearranging for V = Q/C, substituting Q/C for each
capacitor voltage VC in the above KVL equation will give us:
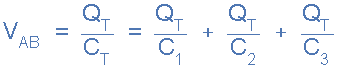 circuit current
dividing each term through by Q gives
circuit current
dividing each term through by Q gives
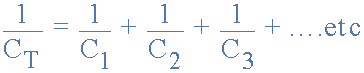 capacitors in series equation
When adding together Capacitors in Series, the reciprocal ( 1/C ) of the
individual capacitors are all added together ( just like resistors in
parallel ) instead of the capacitance’s themselves. Then the total value
for capacitors in series equals the reciprocal of the sum of the reciprocals
of the individual capacitances.
capacitors in series equation
When adding together Capacitors in Series, the reciprocal ( 1/C ) of the
individual capacitors are all added together ( just like resistors in
parallel ) instead of the capacitance’s themselves. Then the total value
for capacitors in series equals the reciprocal of the sum of the reciprocals
of the individual capacitances.
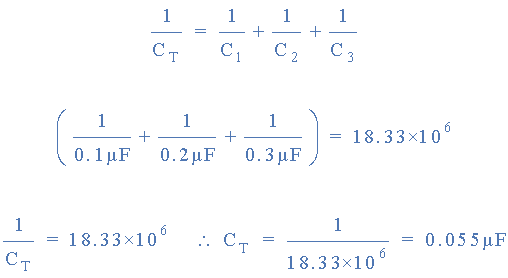 total series capacitance
One important point to remember about capacitors that are connected together
in a series configuration. The total circuit capacitance ( CT ) of any
number of capacitors connected together in series will always be LESS than
the value of the smallest capacitor in the series string. In our example
above, the total capacitance CT was calculated as being 0.055μF but the
value of the smallest capacitor in the series chain is only 0.1μF.
This reciprocal method of calculation can be used for calculating any number
of individual capacitors connected together in a single series network. If
however, there are only two capacitors in series, then a much simpler and
quicker formula can be used. This is given as:
total series capacitance
One important point to remember about capacitors that are connected together
in a series configuration. The total circuit capacitance ( CT ) of any
number of capacitors connected together in series will always be LESS than
the value of the smallest capacitor in the series string. In our example
above, the total capacitance CT was calculated as being 0.055μF but the
value of the smallest capacitor in the series chain is only 0.1μF.
This reciprocal method of calculation can be used for calculating any number
of individual capacitors connected together in a single series network. If
however, there are only two capacitors in series, then a much simpler and
quicker formula can be used. This is given as:
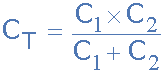 total capacitance in series
If the two series connected capacitors are equal and of the same value, that
is: C1 = C2, we can simplify the above equation further as follows to find
the total capacitance of the series combination.
total capacitance in series
If the two series connected capacitors are equal and of the same value, that
is: C1 = C2, we can simplify the above equation further as follows to find
the total capacitance of the series combination.
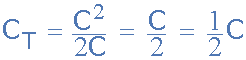 equal value capacitors
Then we can see that if and only if the two series connected capacitors are
the same and equal, then the total capacitance, CT will be exactly equal to
one half of the capacitance value, that is: C/2.
With series connected resistors, the sum of all the voltage drops across the
series circuit will be equal to the applied voltage VS ( Kirchhoff’s
Voltage Law ) and this is also true about capacitors in series.
With series connected capacitors, the capacitive reactance of the capacitor
acts as an impedance due to the frequency of the supply. This capacitive
reactance produces a voltage drop across each capacitor, therefore the
series connected capacitors act as a capacitive voltage divider network.
The result is that the voltage divider formula applied to resistors can also
be used to find the individual voltages for two capacitors in series. Then:
equal value capacitors
Then we can see that if and only if the two series connected capacitors are
the same and equal, then the total capacitance, CT will be exactly equal to
one half of the capacitance value, that is: C/2.
With series connected resistors, the sum of all the voltage drops across the
series circuit will be equal to the applied voltage VS ( Kirchhoff’s
Voltage Law ) and this is also true about capacitors in series.
With series connected capacitors, the capacitive reactance of the capacitor
acts as an impedance due to the frequency of the supply. This capacitive
reactance produces a voltage drop across each capacitor, therefore the
series connected capacitors act as a capacitive voltage divider network.
The result is that the voltage divider formula applied to resistors can also
be used to find the individual voltages for two capacitors in series. Then:
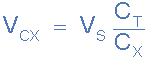 voltage across series capacitors
Where: CX is the capacitance of the capacitor in question, VS is the supply
voltage across the series chain and VCX is the voltage drop across the
target capacitor.
voltage across series capacitors
Where: CX is the capacitance of the capacitor in question, VS is the supply
voltage across the series chain and VCX is the voltage drop across the
target capacitor.
 total series capacitance
total series capacitance
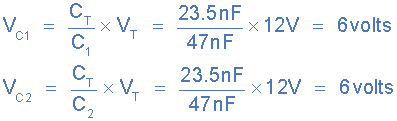 Voltage drop across the two identical 47nF capacitors,
Voltage drop across the two identical 47nF capacitors,
 equal capacitance in series
b) Total Unequal Capacitance,
equal capacitance in series
b) Total Unequal Capacitance,
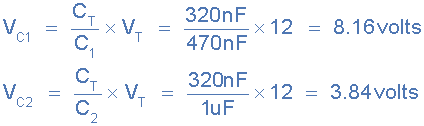 series capacitance
Voltage drop across the two non-identical Capacitors: C1 = 470nF and C2 =
1μF.
series capacitance
Voltage drop across the two non-identical Capacitors: C1 = 470nF and C2 =
1μF.
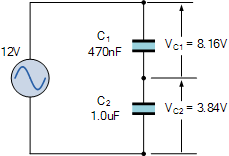 unequal components
capacitor voltage drop
unequal components
capacitor voltage drop
|
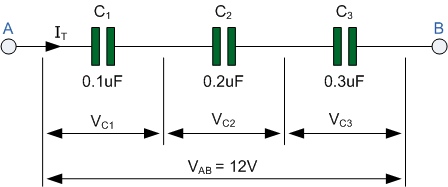
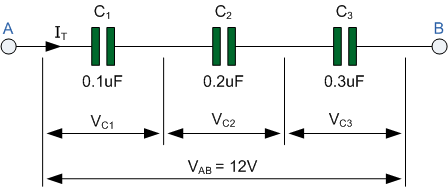
Since Kirchhoff’s voltage law applies to this and every
series connected circuit, the total sum of the individual voltage drops will be equal in value to the supply voltage, VS. Then 8.16 + 3.84 = 12V.
Note also that if the capacitor values are the same, 47nF in our first example, the supply voltage will be divided equally across each capacitor as shown. |
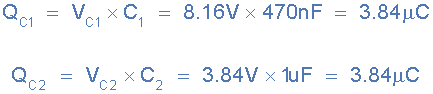 charge
Note that the ratios of the voltage drops across the two capacitors
connected in series will always remain the same regardless of the supply
frequency as their reactance, XC will remain proportionally the same.
Then the two voltage drops of 8.16 volts and 3.84 volts above in our simple
example will remain the same even if the supply frequency is increased from
100Hz to 100kHz.
Although the voltage drops across each capacitor will be different for
different values of capacitance, the coulomb charge across the plates will
be equal because the same amount of current flow exists throughout a series
circuit as all the capacitors are being supplied with the same number or
quantity of electrons.
In other words, if the charge across each capacitors plates is the same, as
Q is constant, then as its capacitance decreases the voltage drop across the
capacitors plates increases, because the charge is large with respect to the
capacitance. Likewise, a larger capacitance will result in a smaller voltage
drop across its plates because the charge is small with respect to the
capacitance.
charge
Note that the ratios of the voltage drops across the two capacitors
connected in series will always remain the same regardless of the supply
frequency as their reactance, XC will remain proportionally the same.
Then the two voltage drops of 8.16 volts and 3.84 volts above in our simple
example will remain the same even if the supply frequency is increased from
100Hz to 100kHz.
Although the voltage drops across each capacitor will be different for
different values of capacitance, the coulomb charge across the plates will
be equal because the same amount of current flow exists throughout a series
circuit as all the capacitors are being supplied with the same number or
quantity of electrons.
In other words, if the charge across each capacitors plates is the same, as
Q is constant, then as its capacitance decreases the voltage drop across the
capacitors plates increases, because the charge is large with respect to the
capacitance. Likewise, a larger capacitance will result in a smaller voltage
drop across its plates because the charge is small with respect to the
capacitance.